平均値や中央値は、どちらも集団の中心的傾向を示す値（代表値）として使われます。ただし、それぞれ計算・算出方法が異なる点に注意が必要です。

本記事では、平均値と中央値の違いを説明した上で、具体例を交えつつ計算方法を紹介します。

平均値と中央値には違いがある

平均値も中央値も、データの中心的傾向を示した数値（代表値）である点で共通していますが、計算方法に違いがあります。そのため、データの分布次第で、平均年収や平均点などの平均値と、中央値の間に大きな差が生じることもあるでしょう。

例えば、厚生労働省によると2021年の1世帯当たり平均所得金額（平均値）が545万7千円に対し、中央値は423万円です。つまり、平均値の方が中央値よりも100万円以上上回っています。

参考：厚生労働省「2022（令和4）年 国民生活基礎調査の概況 各種世帯の所得等の状況」

平均値とは

平均値とは、データの数字をすべて足してから、データの個数で割った数値のことです。平均値の求め方や計算例、平均値の種類を紹介します。

平均値の求め方

平均値を求めるには、データの数字をひとつずつ足してから、その個数で割ることがポイントです。データ「a,b,c,d,e, ……」の平均値を求める場合、以下の式で計算します。

・平均値＝（a＋b＋c＋d＋e＋……）÷データの個数

仮に平均値を出すのが（a, b, c, d, e）までの範囲であれば、データの個数は「5（個）」です。一方「a, b, c, d, e, f, g」の範囲で平均値を出す場合は「7」で割ります。

平均値の計算・算出例

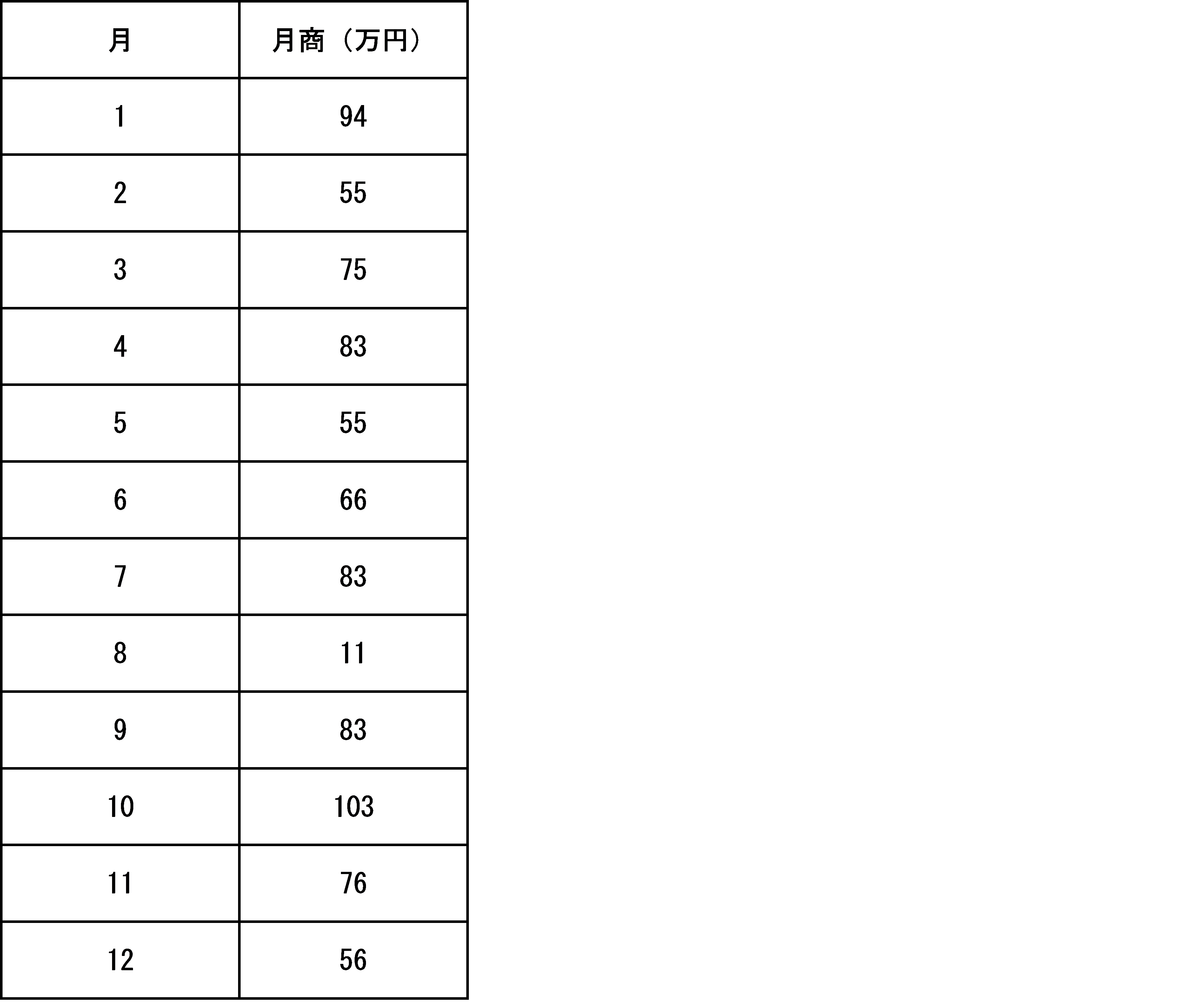
ある年の1月から12月までの月商が以下のとおりのA社の、平均月商を計算してみましょう。

（94＋55＋75＋83＋55＋66＋83＋11＋83＋103＋76＋56）÷12＝70

つまり、A社のある年の月商の平均値（平均月商）は70万円です。

平均値の種類

平均値には、以下のようにさまざまな種類があります。

・算術平均（相加平均）
・相乗平均
・調和平均
・二乗平均
・加重平均

算術平均は、ここまで紹介してきた数値を足し合わせて平均を出すことです。一般的に、平均値は算術平均のことを指します。

相乗平均とは、数字を掛け合わせて平均を出すことです。（a, b）のデータがある場合、算術平均は「（a＋b）÷2」で計算するのに対し、相乗平均は「abの平方根」を計算します。

調和平均とは、数値の逆数をとってから算術平均で平均値を出し、また逆数をとる値です。二乗平均とは、各数値を二乗してから算術平均で算出した値を指します。

加重平均とは、各数値の重要度に合わせて重みを加味した上で、算術平均で計算した値です。