中央値とは

中央値とは、母集団（調査対象になるものの全体）の分布の中央に位置する値のことです。ここから、中央値の求め方や計算例を確認していきましょう。

中央値の求め方

中央値を求める際は、データを小さい順（大きい順）に並び替えて、真ん中の値を見つけることがポイントです。

例えば「2, 3, 5, 40, 100」のデータでは、真ん中の「5」が中央値と判断できます。同データで、平均値は「30」のため、今回のケースでは中央値の方が小さいことがわかるでしょう。

なお、個数が偶数の場合は真ん中に数値が2つ出現します。偶数の場合は、真ん中の2つの数値の平均値が中央値です。

中央値の計算・算出例

平均値と同じく、A社のある年の月商データを使って、中央値を計算してみましょう。

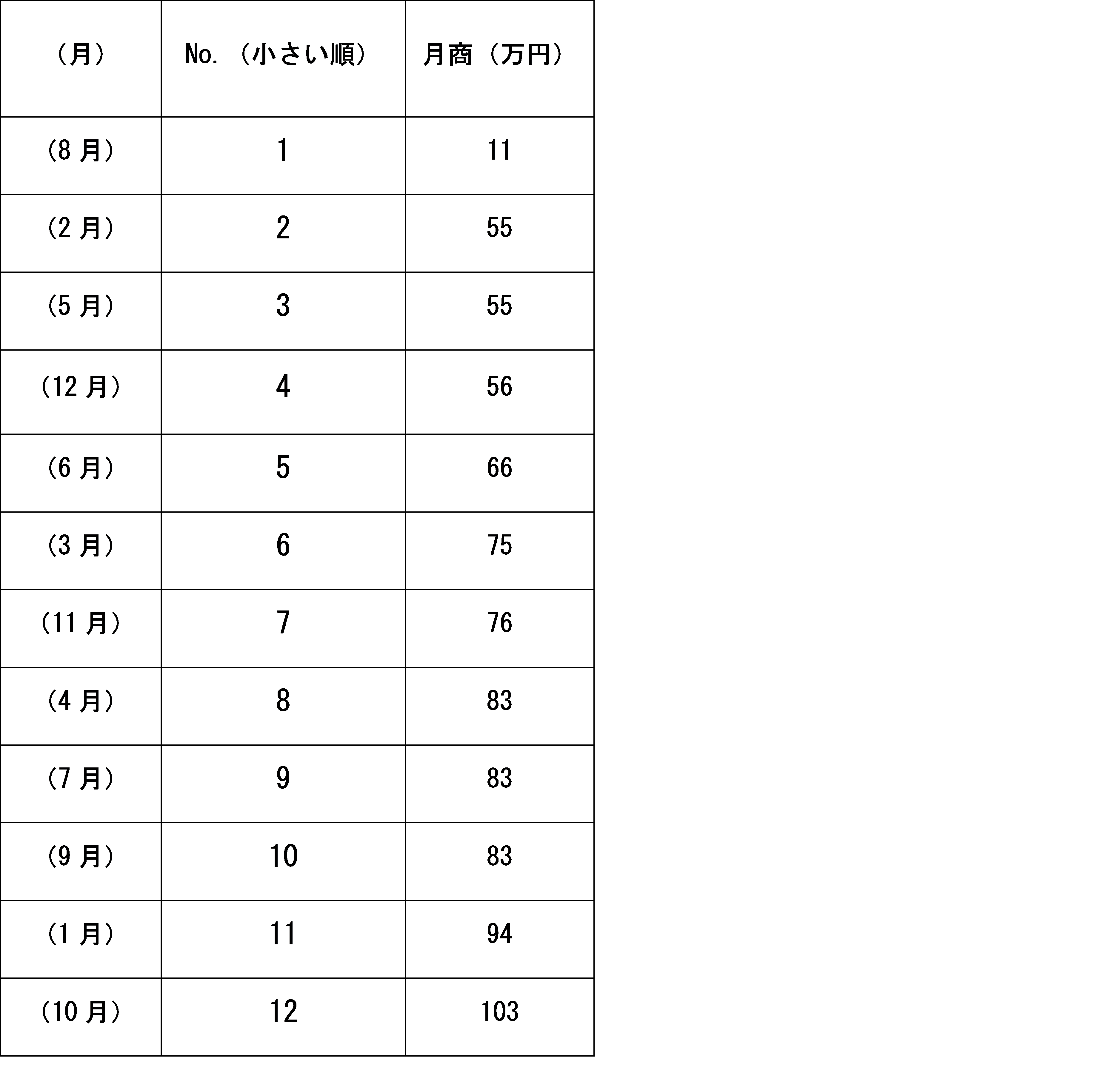
まず、中央値を小さい順に並べ替えます。

A社の月商を並べ替えた結果、真ん中の数値（No.6とNo.7）は「75万円（3月）」と「76万円（11月）」でした。そのため、中央値は75.5万円と計算できます（（75万円 ＋ 76万円）÷2）。

平均値と中央値以外に最頻値（モード）も重要

平均値や中央値以外に、代表値として「最頻値（モード）」を用いることがあります。最頻値とは、データの中で最も頻繁に出現する値のことです。

最頻値の求め方や、計算例を解説します。

最頻値の求め方

最頻値を求める際は、同じ数値をまとめて、最も多く出現した数値の数を数えることがポイントです。

「5, 2, 3, 5, 7, 9, 5」のデータでは「2」「3」「7」「9」はそれぞれ1個しかありませんが、「5」は3つあります。よって「5, 2, 3, 5, 7, 9, 5」の最頻値は「5」です。

なお、このデータの平均値は約「5.14」、中央値は「5」と計算できます。

最頻値の計算・算出例

A社のある年の月商の最頻値も計算してみましょう。

表を確認すると「55万円」が2回、「83万円」が3回出現していることがわかります（そのほかの数字は各1回）。つまり、A社のある年の月商の最頻値は「83万円」です。

なお、A社のある年における月商の平均値が「70万円」、中央値が「75.5万円」、最頻値が「83万円」でそれぞれ異なります。どの値を代表値としてとらえるかによって、A社に対するイメージが変わるでしょう。