標準偏差の意味

標準偏差とは、データのばらつきを示したものです。標準偏差を見れば、対象データの偏差の目安がわかるでしょう。

分散もばらつきを示した指標ですが、偏差を「2乗」してから合計しているため、元のデータと単位が異なっています。そこで「2乗」されている分散の平方根をとることで、元のデータの単位に揃えたのが標準偏差です。

例えば、X地域にある会社の従業員数の分散（323.6）の平方根をとれば、標準偏差を計算できます（約18）。平方根をとる際は、電卓で分散の数値を入力してから「ルート」ボタンを押しましょう。

なお、標準偏差が小さければ対象データのばらつきが小さく、標準偏差が大きければ対象データのばらつきが大きいことを意味します。

標準偏差の求め方

標準偏差の求め方は、以下のとおりです。

1. 平均値を計算する
2. 偏差を計算する
3. 分散を計算する
4. 分散の平方根を計算する

つまり、1〜3の手順でまず分散を求めてから、その平方根を計算すれば標準偏差を算出できます。

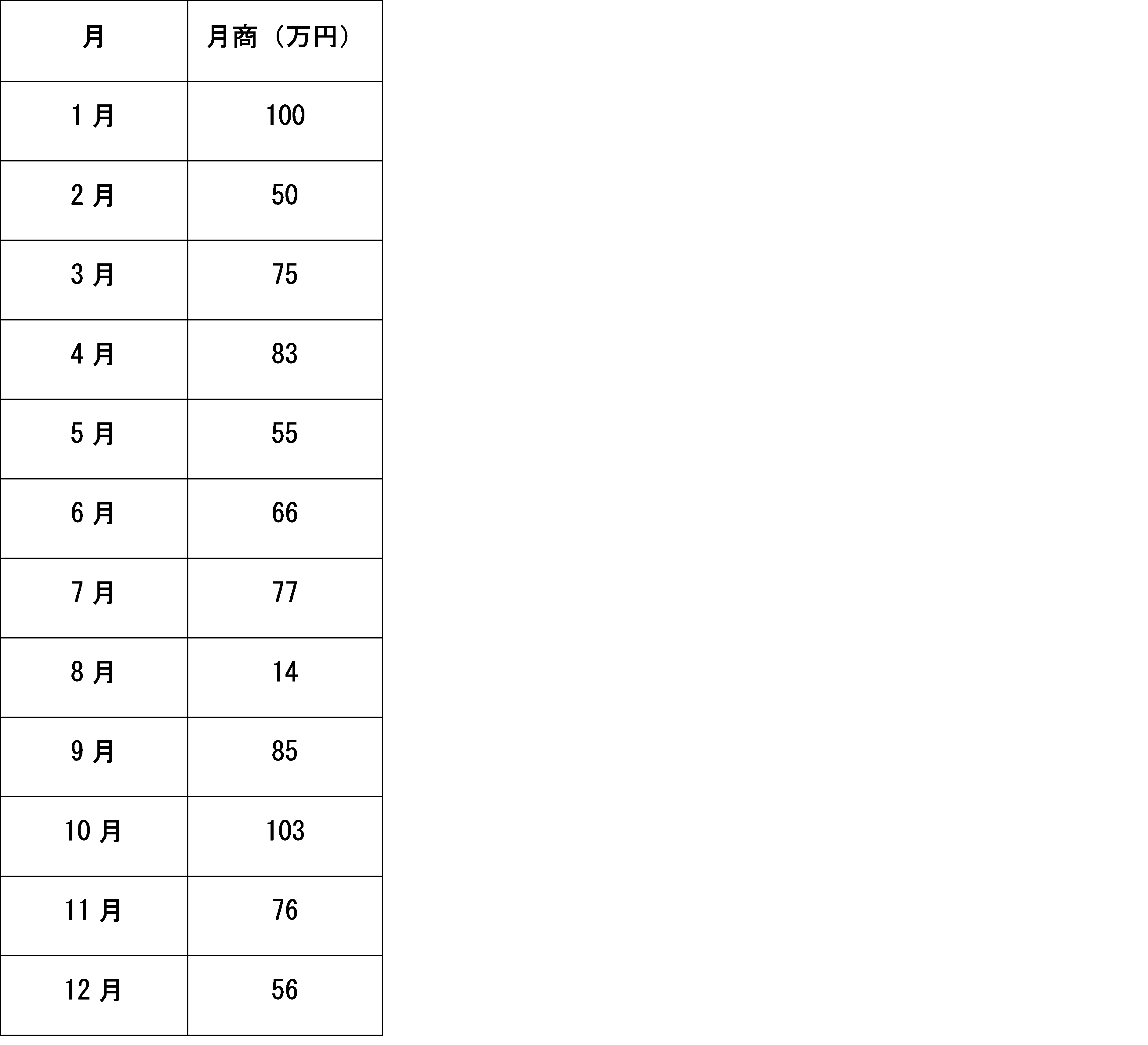
A社のある年度の月商データ（以下図表）を使い、標準偏差を求めてみましょう。

1. 平均値を計算する

各月の月商を合計して、個数（今回は12か月）で割ることで平均値を計算できます。

・（100＋50＋75＋83＋55＋66＋77＋14＋85＋103＋76＋56）÷12＝70

つまり、A社の平均月商（月商の平均値）は70万円です。

2. 偏差（へんさ）を計算する

偏差は各月商から平均値を計算することで求められます。例えば、1月の偏差は「30」（100ー70）2月は「ー20」（50ー70）、3月は「5」（75ー70）です。

なお、偏差の合計は必ず0になります。そのため、分散や偏差値を計算する際にはあらかじめ偏差を2乗しなければなりません。今回各月の偏差を2乗すると、「900・400・25・169・225・16・49・3136・225・1089・36・196」となります。

3. 分散を計算する

分散を計算するには、まず偏差を2乗した値を合計しなければなりません。

・900＋400＋25＋169＋225＋16＋49＋3136＋225＋1089＋36＋196＝6,466

続いて、合計をデータの個数（今回は12か月）で割ります。

・6,466÷12≒539

よって、A社のある年度の月商データの分散は「539」です。

4. 分散の平方根を計算する

分散まで求めれば、後はその平方根を計算するだけで標準偏差がわかります。電卓で、「539」と入力してから「ルート」ボタンを押してみましょう（先に「ルート」ボタンを押す電卓もあります）。

ここまでの計算で、23.21……という値が出たでしょう。つまり、A社のある年度の月商データの標準偏差はおよそ「23」です。